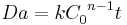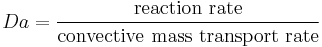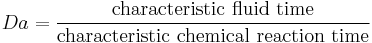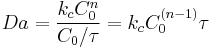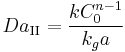Damköhler numbers
The Damköhler numbers (Da) are dimensionless numbers used in chemical engineering to relate chemical reaction timescale to other phenomena occurring in a system. It is named after German chemist Gerhard Damköhler (1908–1944).
There are several Damköhler numbers, and their definition varies according to the system under consideration.
For a general chemical reaction A → B of nth order, the Damköhler number is defined as
where:
- k = kinetics reaction rate constant
- C0 = initial concentration
- n = reaction order
- t = time
and it represents a dimensionless reaction time. It provides a quick estimate of the degree of conversion ( ) that can be achieved in continuous flow reactors.
) that can be achieved in continuous flow reactors.
Generally, if 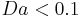 , then
, then 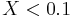 . Similarly, if
. Similarly, if 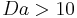 , then
, then  .[1]
.[1]
In continuous or semibatch chemical processes, the general definition of the Damköhler number is:
or as
For example, in a continuous reactor, the Damköhler number is:
where  is the mean residence time or space time.
is the mean residence time or space time.
In reacting systems that include also interphase mass transport, the second Damköhler number (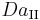 ) is defined as the ratio of the chemical reaction rate to the mass transfer rate
) is defined as the ratio of the chemical reaction rate to the mass transfer rate
where
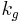 is the global mass transport coefficient
is the global mass transport coefficient is the interfacial area
is the interfacial area
Related Links
References
|
|||||